
ΣΥΝΘΕΤΙΚΗ ΔΗΜΙΟΥΡΓΙΚΗ ΕΡΓΑΣΙΑ
στο μάθημα των ΜΑΘΗΜΑΤΙΚΩΝ
από τους μαθητές της Α' τάξης του Πειραματικού Λυκείου Μυτιλήνης
Δ. ΚΟΝΤΕΛΛΗ - Μ. ΚΟΡΔΩΝΗ
Καθηγητής ανάθεσης-παρακολούθησης : Δημ ΤσουπίδηςΜυτιλήνη - Άνοιξη 1999
ΠΡΟΛΟΓΟΣ
Κατά τη διάρκεια της ιστορίας, αρκετοί λαοί ανέπτυξαν ένα δικό τους σύστημα αρίθμησης, είτε δανείστηκαν αντίστοιχα άλλων λαών κάνοντας κάποιες τροποποιήσεις σ’αυτά. Σ’ αυτήν την εργασία θα προσπαθήσουμε να αναλύσουμε τα διάφορα συστήματα αρίθμησης του κάθε λαού από την αρχαιότητα μέχρι το πρόσφατο παρελθόν.
Γενικά
Ο άνθρωπος από πολύ νωρίς, ασφαλώς από την εποχή που δημιούργησε τα πρώτα ποίμνια από εξημερωμένα ζώα, χρησιμοποίησε σύμβολα για να συμβολίζει αριθμούς: την τελεία ή ένα μικρό ευθύγραμμο τμήμα για το ένα, ένα πρόχειρο σχήμα του χεριού για το πέντε, το σχήμα δύο χεριών για το δέκα ( πράγματι το ρωμαϊκό πέντε,
V είναι ένα σχηματοποιημένο χέρι, το ρωμαϊκό δέκα, Χ, δύο σχηματοποιημένα χέρια ). Όλα αυτά όμως δεν μπορεί να χαρακτηριστούν ένα κάποιο σύστημα αρίθμησης. Οι αρχαίοι Έλληνες, οι οποίοι, άλλωστε, είναι εκείνοι, που θεμελίωσαν τα μαθηματικά ως πραγματική επιστήμη, χρησιμοποιούσαν για αριθμητικά σύμβολα τα γράμματα του αλφαβήτου τους, αλλά δεν εξεπόνησαν ένα κατάλληλο σύστημα για την παράσταση κάθε αριθμού με έναν περιορισμένο αριθμό συμβόλων. Είναι, παρόλ’ αυτά γεγονός ότι η αρχή της “ θέσης ” ήταν ήδη σε χρήση κατά την κλασσική αρχαιότητα στον άβακα και στα λογιστικά πινάκια, που χρησιμοποιούσαν για τους εμπορικούς λογαριασμούς. Παρά τις τελειοποιήσεις του άβακα στο Μεσαίωνα, έλειπε ένα σύμβολο για το “ μηδέν ”. Το σύμβολο αυτό εισήγαγαν οι Ινδοί και τελειοποίησαν τη χρήση του οι Άραβες, οι οποίοι και μετάδωσαν τη γραφή των αριθμών, που χρησιμοποιείται σήμερα στην Ευρώπη και χαρακτηρίζεται ως αραβική ή ινδική ή αραβοινδική. Παρόλ’ αυτά χρειάστηκαν 2 αιώνες (13ος – 15ος) για να επικρατήσει η αραβική αρίθμηση θέσης. Τα αρχαιότερα γραπτά με αριθμούς φέρουν το αποτύπωμα των δέκα δακτύλων (στα αρχαία ιερατικά γραπτά κυρίως των μεσογειακών φυλών οι αριθμοί από το ένα ως το εννιά παριστάνονται μ’ αυτόν τον τρόπο).
Ειδικότερα
α) Σουμέριοι
Μαζί με τους Αιγυπτίους θεωρούνται οι πρώτοι που χρησιμοποίησαν τους αριθμούς παράλληλα με τη γραφή . Αυτό έγινε πριν από πέντε χιλιάδες χρόνια στη χώρα που ονομάζεται σήμερα Ιράκ . Η χώρα αυτή διασχίζεται από δύο μεγάλα ποτάμια , τον Τίγρη και τον Ευφράτη . ΟΙ αριθμοί ήταν απαραίτητοι για τη συγκέντρωση των φόρων που χρησιμοποιούνταν για το χτίσιμο πόλεων, ναών και αρδευτικών συστημάτων . Αυτοί που κρατούσαν τα αρχεία ήταν οι ιερείς και ήταν αναγκαίο να χρησιμοποιούν σημάδια για να δείχνουν κάθε στιγμή την κατάσταση της φορολογίας . Μια από τις σημαντικότερες σειρές σημαδιών που έπρεπε να βρουν, ήταν οι αριθμοί. Για κάθε αριθμό θα μπορούσε να φτιαχτεί και ένα διαφορετικό σημάδι, αλλά υπάρχουν τόσοι πολλοί διαφορετικοί αριθμοί, που σημαίνει ότι θα έπρεπε να θυμάται κανείς χιλιάδες διαφορετικά σημάδια. Χαρακτηριστικό τους ήταν έγραφαν τους αριθμούς από τα δεξιά προς τα αριστερά. Δυστυχώς δε σώζονται αρκετά δείγματα αρίθμησης και δεν μπορούμε να έχουμε μια ολοκληρωμένη εικόνα. Φαίνεται να έδωσαν ιδιαίτερη σημασία στο εξήντα, λόγω του πλήθους των αριθμών με τους οποίους μπορεί να διαιρεθε ί
.
β) Αιγύπτιοι
Οι αρχαίοι Αιγύπτιοι την αριθμητική την παρέλαβαν από τους Βαβυλώνιους.
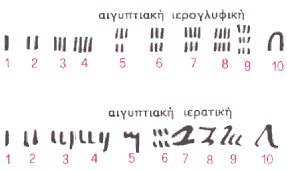
Δημιούργησαν 2 είδη γραφής, την αιγυπτιακή ιερογλυφική και την αιγυπτιακή ιερατική. Ήταν οι πρώτοι που παρίσταναν τον κάθε αριθμό με το ίδιο κατακόρυφο σημάδι, που μοιάζει με δάκτυλο. Έφτιαξαν το σημάδι Ι για να παριστάνουν τον αριθμό ένα.
Είχαν έναν ορισμένο τρόπο για να γράφουν τα σύμβολα. π.χ. Για το πέντε δεν έγραφαν ΙΙΙΙΙ αλλά έγραφαν ΙΙΙ και αμέσως από κάτω ΙΙ. Ήταν πιο εύκολο να δει κανείς τρία σημάδια στη σειρά και έπειτα δυο ξέχωρα σημάδια, από το να διακρίνει πέντε σημάδια στην ίδια σειρά. Κάτι παρόμοιο κάνουμε κι εμείς σήμερα για το πέντε£ Επίσης για το δέκα χρησιμοποιούσαν ένα σύμβολο σαν ανάποδο U. Επίσης σκέφτηκαν ότι δε χρειάζεται να γραφεί ή να μετρηθεί περισσότερο από εννιά φορές ένα σύμβολο και έτσι επινόησαν ένα καινούργιο σύμβολο για κάθε φορά που έπρεπε να γραφεί κάποιο σύμβολο δέκα φορές. Έτσι χρησιμοποίησαν ένα σύμβολο σαν σπείρα που μοιάζει λίγο με αυτό: 9. Έτσι συμπεραίνουμε ότι έδωσαν ιδιαίτερη σημασία στον αριθμό δέκα και ότι για τους αριθμούς από το 1 μέχρι 999 δεν χρειαζόταν να θυμούνται παρά τρία σύμβολα. Επίσης έπρεπε να βρεθεί ένα καινούργιο σύμβολο για το χίλια , το δέκα χιλιάδες κ.ο.κ.
Στήλη του 1450 π.Χ. με αιγυπτιακή ιερογλυφική γραφή, στα σημεία που είναι χρωματισμένα διακρίνονται αριθμητικά σύμβολα.

Μ’ αυτή τη μέθοδο βρίσκουμε ένα καινούργιο σύμβολο κάθε φορά που χρειαζόμαστε δέκα από τα μικρότερα σύμβολα.
Πρόβλημα παραμένει αν γνώριζαν ή όχι και το δεκαδικό σύστημα. Οπωσδήποτε είναι γνωστό ότι δεν γνώριζαν το 0. Χρησιμοποιούσαν όμως τις κλασματικές μονάδες , όπως το ½. Επίσης γνώριζαν την τιμή του π=3,14 .
γ) Κινέζοι
Από την αρχή η κινεζική αριθμητική συσχετιζόταν με τα μαντεία. Οι αριθμοί που χρησιμοποιούνται συνήθως σήμερα βρέθηκαν επάνω σε μαντικά οστά και θυρέους χελώνας, χρονολογούμενα από την περίοδο του Σαγκ καθώς και επάνω σε ορειχάλκινα αντικείμενα και νομίσματα της περιόδου Τσου. Δεν υπήρχε το 0, το οποίο δεν χρησιμοποιήθηκε πριν από τον 15ο αιώνα π.Χ. Χρησιμοποιούσαν αυστηρή δεκαδική σημειογραφία, πράγμα που καθιστά το κινεζικό αριθμητικό σύστημα τελείως ανεξάρτητο από εκείνο που χρησιμοποιήθηκε στη Μεσοποταμία. Είχαν υπολογίσει το π με πολύ υψηλό αριθμό ακρίβειας, δίνοντάς του ανώτερες και κατώτερες τιμές όπως 3,1415927 και 3,1415926.
δ) Πολιτισμοί Μεσοαμερικής
Οι Μάγιας και οι Αζντέκοι, δύο λαοί που έζησαν στο Μεξικό πριν φτάσουν εκεί οι Ευρωπαίοι, χρησιμοποίησαν ένα αριθμητικό σύστημα που βασιζόταν στον αριθμό 20. Έτσι το σύστημα αρίθμησής τους αύξανε εικοσαδικά από τα κάτω προς τα πάνω. Γνώριζαν τη χρήση του μηδενικού και έτσι μπορούσαν να γράφουν εύκολα αριθμούς που αντιπροσώπευαν οποιαδήποτε αξία. Το ίδιο εύκολα έκαναν προσθέσεις κι αφαιρέσεις. Σε αντίθεση με αυτούς τους δύο λαούς, οι Ίνκας, ο
τρίτος σημαντικός πληθυσμός που αναπτύχθηκε στην περιοχή, δεν γνώριζαν τη γραφή και τους αριθμούς και γι’αυτό δεν άφησαν γραπτά μνημεία.ε) Ινδοί
- ΙνδουιστέςΟι Ινδουιστές στην Ινδία δημιούργησαν ένα τέτοιο σύνολο από σύμβολα για τους αριθμούς, που το χρησιμοποιούμε ακόμη και σήμερα. Οι μορφές των συμβόλων που χρησιμοποιούμε σήμερα δεν είναι ακριβώς ίδιες με αυτές που χρησιμοποιούσαν οι Ινδουιστές πριν από πολλούς αιώνες. Παρόλ’ αυτά, αν παρατηρούμε τους Ινδουιστικούς αριθμούς, μπορούμε να σε αυτούς τις πρώτες αρχές των αριθμητικών συμβόλων που χρησιμοποιούμε και σήμερα. Από τους Ινδουιστές μαθαίνουμε τα εξής: 1=ένα, 2=δύο, 3=τρία, 4=τέσσερα, 5=πέντε, 6=έξι, 7=επτά, 8=οχτώ, 9=εννιά.Οι αριθμοί αυτοί ή οι αρχικοί τους πρόγονοι εμφανίστηκαν για πρώτη φορά στην Ινδία πριν από δύο χιλιάδες διακόσια χρόνια περίπου.
Μπορεί να αναρωτηθεί κανείς, βέβαια, πώς φτάσαμε στο σημείο να χρησιμοποιούμε τους ίδιους αριθμούς με τους Ινδουιστές. Στο κάτω κάτω, δεν είναι και αυτοί οι αριθμοί άλλο ένα από τα τόσα συστήματα συμβόλων; Δε θα ήταν προτιμότερο να παραμείνουν οι άνθρωποι στα παλιά σύμβολα, όπως τα ρωμαϊκά σύμβολα στα οποία ήταν συνηθισμένοι;
Βέβαια οι άνθρωποι θα προτιμούσαν κάτι τέτοιο και, πράγματι, έμειναν πιστοί στα παλιά σύμβολα όσο γινόταν περισσότερο. Ο
λόγος, όμως, για τον οποίο οι αριθμοί των Ινδουιστών άρχισαν να εξαπλώνονται πέρα από την Ινδία, ήταν ότι οι Ινδουιστές είχαν κάποια καλύτερη ιδέα. Στην αρχή οι Ινδοί (όπως και οι Αιγύπτιοι) έφτιαχναν καινούργια σύμβολα για αριθμούς μεγαλύτερους από εννέα. Είχαν διαφορετικά σύμβολα για το δέκα, το είκοσι, το τριάντα κλπ., όπως επίσης και για το εκατό, το διακόσια, το τριακόσια κ.ο.κ. Βρέθηκε, όμως, κάποιος (φυσικά δεν γνωρίζουμε ποιος) που αναρωτήθηκε αν αυτό ήταν απαραίτητο. Ο αριθμός διακόσια σημαίνει δύο φορές το “εκατό”. Ο αριθμός είκοσι σημαίνει δύο “δέκα” και ο αριθμός δύο σημαίνει δύο φορές το “ένα”. Σε κάθε περίπτωση ο αριθμός σήμαινε δύο φορές κάτι. Ας πούμε ότι παίρνουμε την απόφαση πως το σύμβολο στο δεξιό άκρο του αριθμού μας δείχνει πόσες μονάδες έχει ο αριθμός. Το σύμβολο στα αριστερά του μας δείχνει πόσες δεκάδες υπάρχουν, το αμέσως επόμενο σύμβολο στα αριστερά μας δείχνει πόσες εκατοντάδες υπάρχουν κ.ο.κ. Η σημασία που έχει ένα σύμβολο εξαρτάται από τη θέση στην οποία βρίσκεται. Μ’ αυτό τον τρόπο, τα εννιά ινδουιστικά ψηφία –1,2,3,4,5,6,7,8,9- πρέπει να είναι αρκετά για να γράφουμε τους αριθμούς.Πώς θα μπορούσε ,όμως , να είναι κανείς σίγουρος ότι το διάστημα ανάμεσα στα ψηφία αντιπροσωπεύει δύο κενές θέσεις; Μπορεί να θεωρηθεί ότι δείχνει μόνο μία ή και τρεις κενές θέσεις. Όχι, δεν είναι αρκετό να αφήνει κανείς κενό ανάμεσα στα ψηφία. Πρέπει να βρεθεί κάποιο σύμβολο που να σημαίνει “καθόλου μονάδες” ή “καθόλου εκατοντάδες”.Παρόλα αυτά, αποδείχτηκε πολύ δύσκολο πράγμα το να αντιληφτούμε ότι χρειάζεται ένα τέτοιο σύμβολο. Χρειάστηκαν χιλιάδες χρόνια από τότε που άρχισαν τα ανθρώπινα όντα να χρησιμοποιούν αριθμητικά σύμβολα για να σκεφτεί κάποιος ότι πρέπει να γράψει ένα σύμβολο που να δείχνει το “τίποτα”, το “μηδέν”.Δεν ξέρουμε ακριβώς ποιος ήταν αυτός που σκέφτηκε τελικά να χρησιμοποιήσει ένα τέτοιο σύμβολο. Πιστεύουμε ότι πρέπει να ήταν κάποιος Ινδουιστής και δεν ξέρουμε με σιγουριά πότε συνέβη αυτό. Πιθανόν να έγινε πριν από χίλια τριακόσια χρόνια περίπου. Το σύμβολο που χρησιμοποιούμε σήμερα για το “μηδέν” είναι ένας σκέτος κύκλος, χωρίς τίποτα μέσα του. Το γράφουμε με 0. Οι Ινδουιστές το έλεγαν “σούνια”, που σημαίνει τίποτα.
Μπορεί το 0 που χρησιμοποιούμε σήμερα, να είναι δημιούργημα των Ινδών, όμως το γεγονός ότι το γνωρίζουμε οφείλεται στους Άραβες, οι οποίοι αφού το γνώρισαν από τους Ινδούς διέδωσαν τη χρήση του στη Δύση.
Η επιστήμη των μαθηματικών εθεωρείτο συχνότατα στην Ινδία ως παρακλάδι της αστρονομίας και τα ονόματα των μεγάλων μαθηματικών είναι τα ίδια τα ονόματα των μεγάλων αστρονόμων.
Οι Ινδοί χρησιμοποίησαν κάποιους ειδικούς κανόνες οι οποίοι προϋπόθεταν ότι ο αριθμός γραφόταν με δεκαδική σημειογραφία, με την πρέπουσα σπουδαιότητα αποδιδόμενη στη θέση του μηδενός και της υποδιαστολής. Η χρήση του δεκαδικού συστήματος στάθηκε η προϋπόθεση όλων των προόδων που επακολούθησαν στα μαθηματικά Αυτή η θεμελιώδης ανακάλυψη δόθηκε στον κόσμο από τους Ινδούς αλλά δεν είναι γνωστό ποια χρονολογία. Υποτέθηκε ότι η αρχή της δεκαδικής σημειογραφίας θα μπορούσε να έχει προέλθει από τη Βαβυλώνα, Αλλά δεν θα πρέπει να απορριφθεί η υπόθεση ότι είχε ίσως ξαναεφευρεθεί. Η ιδέα ενός τέτοιου συστήματος μπορούσε να έλθει φυσικά σε καθένα που έχει συνηθίσει, όπως οι Ινδοί, να κάνει ταχυδακτυλουργίες με δυνάμεις του 10. Ο ίδιος ο Αργιαμπχάτα εφεύρε ένα σύστημα στο οποίο οι δυνάμεις του 10 έως το 10 εις την δεκάτη σημειώνονται με μόνο ένα σημείο. Στην αριθμητική, η μέθοδος των τριών ήταν γνωστή, και οι σύνθετες μέθοδοι ονομάζονταν μέθοδος των πέντε, μέθοδος των επτά κ.τ.λ. Επίσης γνωστή ήταν η μέθοδος υπολογισμού του τόκου. Τέλος πιστεύεται ότι οι Ινδοί και κυρίως ο Αργιαμπχάτα ( μαθηματικός ) γνώριζαν τον τρόπο επίλυσης απροσδιορίστων εξισώσεων β΄ βαθμού.
Βλέπουμε έτσι, ότι οι Ινδοί αποδείχτηκαν λαμπροί μαθηματικοί και μάλιστα πραγματοποίησαν ιδιαίτερη πρόοδο στην Άλγεβρα. Οι Άραβες επιστήμονες αναγνώρισαν την οφειλή τους στους Ινδούς και μέσω αυτών η ευρωπαϊκή επιστήμη μπόρεσε να ωφεληθεί από τις ανακαλύψεις των Ινδών μαθηματικών.
στ) Άραβες
Γύρω στο 800 μ.Χ. όχι πολύ αργότερα από τότε που ανακαλύφθηκε το σύμβολο για το 0, τα Ινδουιστικά ψηφία εξαπλώθηκαν στις χώρες βόρεια και δυτικά της Ινδίας. Οι άνθρωποι που κατοικούσαν στις χώρες αυτές μιλούσαν Αραβικά. Αραβόφωνοι λαοί ζούσαν, επίσης, σ’ όλη τη βόρεια Αφρική καθώς και στην Ισπανία. Οι ινδουιστικοί αριθμοί εξαπλώθηκαν σ’ όλο το τμήμα της Αφρικής και από ‘κει στην Ισπανία.
Οι Άραβες ονόμαζαν το σύμβολο για το μηδέν “σιφρ” Οι Ευρωπαίοι ονόμασαν τα αριθμητικά σύμβολα του αραβικού συστήματος αραβικούς αριθμούς ή χαρακτήρες, γιατί είχαν προέλθει από αραβόφωνους λαούς. Οι Ευρωπαίοι, βέβαια , δεν ήξεραν ότι η καταγωγή τους ήταν από την Ινδία. Οι Άραβες δεν επηρεάστηκαν μόνο από τους Ινδούς αλλά δέχτηκαν και την αρχαία ελληνική κληρονομιά. Τέλος, είχαν ανακαλύψει μεθόδους για την απλοποίηση εξισώσεων.
Δηλαδή, οι Άραβες δεν ανακάλυψαν ένα δικό τους σύστημα αρίθμησης, αλλά τελειοποίησαν αυτό των Ινδών.
ζ) Αρχαίοι Έλληνες
Οι αρχαίοι Έλληνες δεν έδωσαν λύσεις βιώσιμες στο πρόβλημα παράστασης των φυσικών αριθμών. Χρησιμοποίησαν για την παράσταση των αριθμών το αλφάβητό τους. Οι Έλληνες παρίσταναν τους φυσικούς αριθμούς με δύο τρόπους. Κατά τον ένα για τους 5, 10, 100, 1000 χρησιμοποιούσαν τα γράμματα Π, Δ, Η, Χ δηλαδή τα αρχικά των λέξεων πέντε, δέκα, εκατό, χίλια (το Η ήταν το αρχικό της λέξης εκατό).
Για το πενταπλάσιο ενός αριθμού χρησιμοποιούσαν το σύμβολο του αριθμού κάτω από το Π : έτσι το
Π , Π σήμαινε αντίστοιχα 5*1000 ,5*10. Για το 1 χρησιμοποιούσαν το σύμβολο Ι. Η παράσταση των αριθμών γινόταν με τα γράμματα του τότε αλφαβήτου και με τη χρησιμοποίηση της θέσης του καθενός τους στο αλφάβητο ως εξής :τα α, β, γ, δ, ε, s (στίγμα),ζ, η, θ για τους 1, 2, 3, 4, 5, 6, 7, 8, 9 (μονάδες) , τα ι,κ,λ,μ,ν,ξ,ο,π,7 (“κόππα”) για τους 10, 20, 30, 40, 50, 60, 70, 80, 90 (δεκάδες), τα ρ, σ, τα, υ, φ, χ, ψ, ω, (“σαμπί”) για τους 100, 200, 300, 400, 500, 600, 700, 800, 900 (εκατοντάδες). Κατά την γραφή αυτή ια, ιβ, κγ, ρα κ.λ.π., σήμαιναν αντίστοιχα: 10+1 (=11), 10+2 (=12), 20+3 (=23), 100+1 (=101) κ.λ.π. Το πρόβλημα με αυτό το αριθμητικό σύστημα ήταν ότι δεν ήταν δυνατή η παράσταση μεγάλων αριθμών με έναν περιορισμένο αριθμό συμβόλων.Πραγματικά εξέχουσες ανακαλύψεις στα μαθηματικά ήταν αυτές που έγιναν από τον Πυθαγόρα και τους μαθητές του. Αφορούσαν όχι μόνο τους περιττούς και άρτιους ή τους απλούς και σύνθετους αριθμούς, αλλά τους απλούς αριθμούς που αναφέρονται σε σχήματα, δηλαδή σε αριθμούς που επινοήθηκαν για να παραστήσουν τα σημεία ενός επίπεδου σχήματος ή ενός τρισδιάστατου σχήματος. Διατύπωσαν τη θεωρία των αναλογιών, καθώς και τη θεωρία της αναλογίας των μουσικών διαστημάτων προς το μήκος μιας χορδής σταθερά τεντωμένης. Η Πυθαγόρεια αριθμητική περιλαμβάνει τη θεωρεία των “πλευρικών”, “διαμετρικών
” και “τέλειων” αριθμών και ήταν η πρώτη θεωρεία που καθόρισε τους ασύμμετρους και τους ασύμφωνους αριθμούς.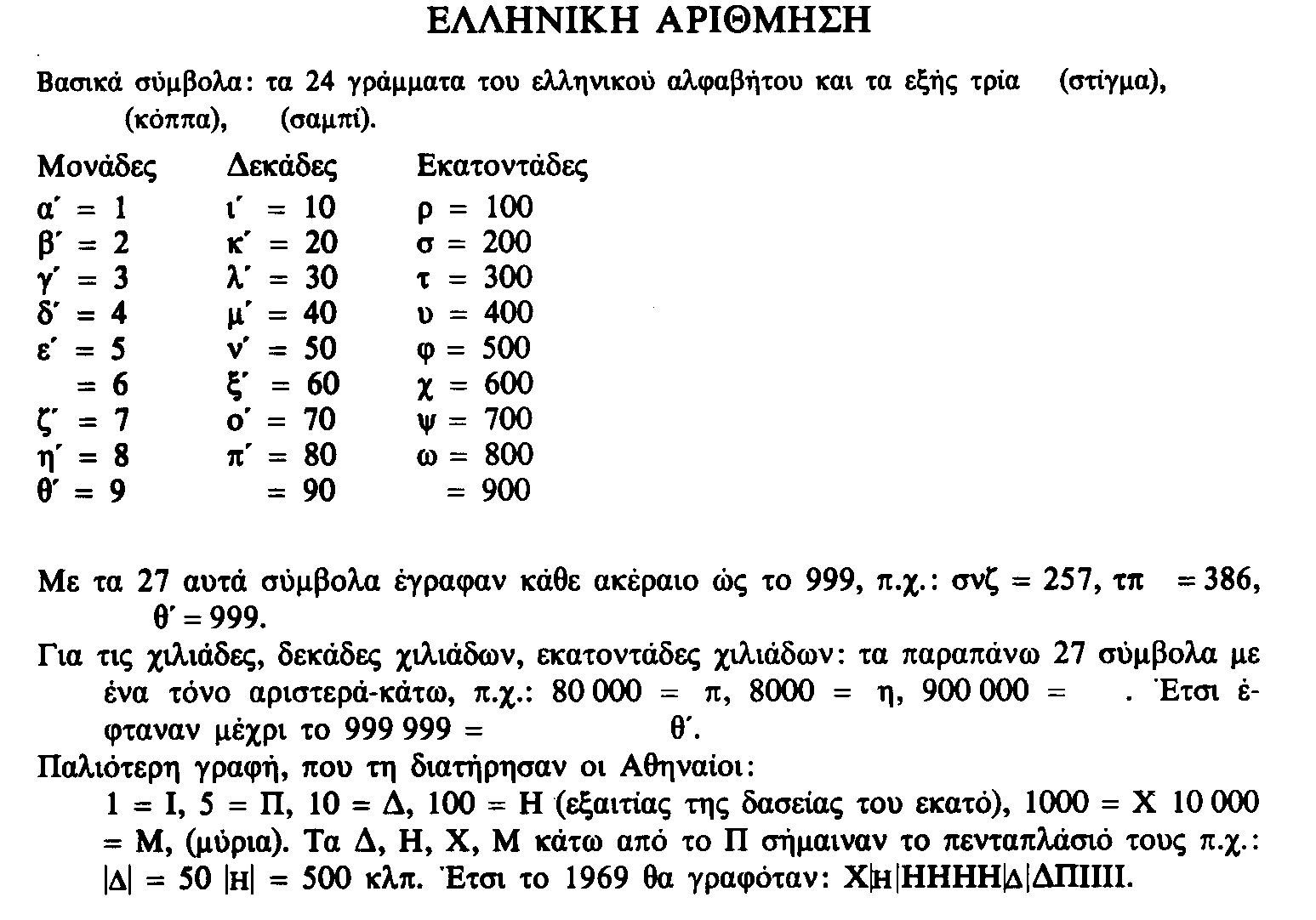
η) Ρωμαίοι
Πριν από δύο χιλιάδες χρόνια περίπου, μεγάλες περιοχές της Ευρώπης, της Ασίας και της Αφρικής εξουσιάζονταν από την Ρώμη. Σ’ αυτή την “Ρωμαϊκή Αυτοκρατορία” χρησιμοποιήθηκε ένα σύστημα αρίθμησης βασισμένο στον αριθμό πέντε. Οι Ρωμαίοι χρησιμοποίησαν σύμβολα που είχαν πάρει από το αλφάβητό τους. Για όλους σχεδόν τους λαούς της Ευρώπης και της Αμερικής που χρησιμοποιούν το ρωμαϊκό αλφάβητο, τα ρωμαϊκά σύμβολα είναι πολύ γνωστά
Οι Ρωμαίοι ξεκίνησαν το σύστημά τους συμβολίζοντας τον αριθμό ένα με Ι. Για το δύο, το τρία και το τέσσερα είχαν τα σύμβολα ΙΙ, ΙΙΙ και ΙΙΙΙ. Μέχρι εδώ το σύστημα αυτό μοιάζει με το αιγυπτιακό σύστημα, μόνο που οι Ρωμαίοι χρησιμοποιούσαν μόνο τέσσερα όμοια σύμβολα προτού φτιάξουν ένα καινούργιο σύμβολο. Αντί να γράφουν το πέντε όπως οι Αιγύπτιοι, ΙΙΙΙΙ, το έγραφαν
V.Αντί να γράφουν το έξι σαν ΙΙΙΙΙΙ έγραφαν VI και για το εννέα έγραφαν VIIII. Αν έγραφαν το δέκα VIIIII, αυτό θα σήμαινε ότι χρησιμοποιήθηκαν πέντε σύμβολα Ι και αυτό δεν επιτρεπόταν. Γι’ αυτό είχαν βρει ένα καινούργιο σύμβολο για το δέκα το Χ. Ο πίνακας των συμβόλων μέχρι το χίλια είναι ο εξής:Ι = ένα |
V= πέντε |
X= δέκα |
L= πενήντα |
C= εκατό |
D= πεντακόσια |
Μ= χίλια |
Επειδή οι Ρωμαίοι χρησιμοποιούσαν ιδιαίτερα σύμβολα για το πέντε, το πενήντα και το πεντακόσια, δεν χρειαζόταν ποτέ να γράφουν περισσότερες από τέσσερις φορές οποιοδήποτε από τα σύμβολα για το ένα, το δέκα και το εκατό. Το είκοσι το έγραφαν ΧΧΙΙ και το εβδομήντα τρία LΧΧΙΙΙ. Το τετρακόσια δεκαοχτώ το έγραφαν CCCCXVIII και το χίλια εννιακόσια ενενήντα εννέα MDCCCCLXXXXVIII.
Αν προσπαθούσαμε να γράψουμε το χίλια εννιακόσια ενενήντα εννέα με το αιγυπτιακό σύστημα θα χρειαζόμασταν ένα σύμβολο του “χίλια” και από εννέα σύμβολα για τα “εκατό” τα “δέκα” και τα “ένα”. Αυτό σημαίνει είκοσι οχτώ σύμβολα συνολικά, ενώ με τα ρωμαϊκά ψηφία θα χρειαζόμασταν μόνο δεκαέξι σύμβολα. Το αιγυπτιακό σύστημα από την άλλη μεριά, χρησιμοποιεί μόνο τέσσερα διαφορετικά είδη συμβόλων, ενώ το ρωμαϊκό σύστημα χρησιμοποιεί εφτά. Με το ρωμαϊκό σύστημα, λοιπόν, χρειάζεται λιγότερο μέτρημα, αλλά περισσότερη απομνημόνευση.
Όταν τα ρωμαϊκά αυτά ψηφία εμφανίστηκαν για πρώτη φορά δεν είχε σημασία με ποια σειρά θα έμπαιναν στον αριθμό. Είτε έγραφε κανείς XVI, είτε IXV ή VIX ήταν το ίδιο πράγμα, δηλαδή ο αριθμός δεκάξι. Ανεξάρτητα, επομένως , από τη σειρά με την οποία πρόσθετε κανείς το δέκα, το πέντε και το ένα, έφτανε πάντα στο δεκαέξι.
Φυσικά είναι πιο εύκολο να γράφει κανείς έναν αριθμό αν βάζει στη σειρά τα σύμβολα με πιο συστηματικό τρόπο. Ο πιο συνηθισμένος τρόπος είναι να ξεχωριστούν και να μπουν μαζί τα ίδια σύμβολα. Το μεγαλύτερο σύμβολο θα είναι στα αριστερά και όσο προχωρούμε προς τα δεξιά γράφουμε όλο και μικρότερα σύμβολα. Ο αριθμός εβδομήντα οχτώ, λοιπόν, θα γράφεται πάντα LXXVIII, κατεβαίνοντας από το L στο Χ, μετά στο V και μετά στο Ι.
Αργότερα οι Ρωμαίοι σκέφτηκαν να ελαττώνουν έναν αριθμό που απεικόνιζαν με ένα ιδιαίτερο σύμβολο. Αφού τα σύμβολα γράφονταν πάντα από τα αριστερά προς τα δεξιά και από το μεγαλύτερο στο μικρότερο, γιατί καμιά φορά να μην αντιστρέφεται η σειρά; Όταν βάζουμε το μικρότερο σύμβολο μετά το μεγαλύτερο, με το συνηθισμένο τρόπο, είναι σαν να προσθέτουμε τα δύο σύμβολα. Επομένως το VI είναι “πέντε και ένα”, δηλαδή έξι. Αν, όμως, βάζουμε το μικρότερο σύμβολο πριν από το μεγαλύτερο, τότε το αφαιρούμε από το μεγαλύτερο. Έτσι το IV είναι “πέντε μείον ένα”, δηλαδή τέσσερα. Το να γράφουμε το τέσσερα IV αντί για ΙΙΙΙ είναι πιο βολικό, γιατί γράφουμε και διαβάζουμε μόνο δύο σύμβολα αντί για τέσσερα. Στην περίπτωση αυτή πρέπει να προσέχουμε τις θέσεις των συμβόλων και να θυμόμαστε ότι κάμουμε αφαίρεση και όχι πρόσθεση. Φυσικά, από τη στιγμή που χρησιμοποιούμε αυτόν τον ιδιαίτερο συμβολισμό για την αφαίρεση, δεν μπορούμε να γράψουμε ανακατωμένα τα σύμβολα. Πρέπει να προσέχουμε που τοποθετούμε ακριβώς το κάθε σύμβολο. Το δυτικό τμήμα της Ρωμαϊκής Αυτοκρατορίας καταλύθηκε πριν από χίλια πεντακόσια χρόνια περίπου. Οι λαοί της δυτικής Ευρώπης εξακολούθησαν να χρησιμοποιούν τα ρωμαϊκά ψηφία για περισσότερο από εφτακόσια χρόνια μετά το τέλος της Ρωμαϊκής Αυτοκρατορίας.
Κατά την ρωμαϊκή γραφή συνεπώς δεν ισχύει το μονοσήμαντο της παράστασης των αριθμών (ο ίδιος αριθμός μπορεί να παρασταθεί με περισσότερους από έναν τρόπους). Αυτό δυσκολεύει την γραφή και εμποδίζει τον αυτοματισμό, γι’ αυτό το λόγο δεν παρουσιάζει πρακτική ωφελιμότητα, ιδιαίτερα όταν πρόκειται για την παράσταση μεγάλων αριθμών και ακόμα δεν επιτρέπει την διατύπωση απλών κανόνων για τη γρήγορη εκτέλεση πράξεων σε αντίθεση με την αρίθμηση θέσης. Τα ίδια μειονεκτήματα παρουσιάζει και η ελληνική γραφή των αριθμών.

θ) Ευρωπαίοι
Οι Ευρωπαίοι αρκούνταν λίγο – πολύ στην αφομοίωση της αρχαίας κληρονομιάς, εμπλουτισμένης από τους Ινδούς και τους Άραβες. Το μεγάλο γεγονός ήταν η εισαγωγή των ονομαζόμενων “αραβικών” αριθμών.
Οι τεχνικές του υπολογισμού, γνωστές τότε ως “λογιστική”, παρέμεναν υποτυπώδεις. Ο Φιμπονάτσι παρέλαβε από τους Άραβες αυτό που παραμένει ακόμη τρέχουσα διαδικασία μας για την αφαίρεση. Ο πολλαπλασιασμός αντιμετωπιζόταν σαν σειρά πράξεων πρόσθεσης και ο διπλασιασμός άλλη μια, χωριστή πράξη. Οι διαδικασίες της διαίρεσης αποτελούσαν πηγή ιδιαίτερης σύγχυσης, ο Γερβέτος παραθέτει ούτε λίγες ούτε πολλές δέκα τέτοιες διαδικασίες και προσφεύγει κατά κύριο λόγο σε μια σειρά από αφαιρέσεις. Ο Φιμπονάτσι, πάντως, μπόρεσε να περιγράψει με λεπτομέρειες μεθόδους για την εξαγωγή τετραγωνικών και κυβικών ριζών.
Αλλά η έννοια των άπειρων ποσοτήτων, που απέρριψε ο Αριστοτέλης αλλά αναγνώρισε ο χριστιανισμός, έβαλε μερικές διάνοιες στον δρόμο προς τον διαφορικό και τον ολοκληρωτικό λογισμό. Δυστυχώς, η δουλειά που έγινε πάνω στη μαθηματική απειρία, γύρω στα 1300, από σοφούς στο Παρίσι ξεχάσθηκε στον δέκατο πέμπτο αιώνα, ώσπου ο Φερμά κι ο Καβαλιέρι την επεξεργάσθηκαν από την αρχή.
| Όνομα Συγγραφέα | Τίτλος Βιβλίου | Τόπος | Ημερο- μηνία | ||
| 1 | Εγκυκλοπαίδεια | “Επιστήμη και Ζωή” | Θεσσαλονίκη | Τόμοι : 2,11 | |
| 2 | Εγκυκλοπαίδεια | “ Νέα Δομή” | Αθήνα | 1996 | Τόμοι : 5,21 |
| 3 | Εγκυκλοπαίδεια | “Ιστορία της Ανθρωπότητας” | Αθήνα | 1970 | Τόμοι : 4,9 |
| 4 | Παν. Ν. Μάγειρα | “Εισαγωγή εις την αριθμοθεωρείαν” | Αθήνα | 1981 | Μέρος Ά ΄Γ έκδοση |
| 5 | Kleiner Morris | “Τα μαθηματικά στο δυτικό πολιτισμό” | Αθήνα | 1985 | Τόμος Ά |
| 6 | Ασίμωφ Ισαάκ | “ Πώς βρήκαμε τους αριθμούς” | (δεν αναφερόταν) | ||
| 7 | Εγκυκλοπαίδεια | “Μεγάλη Εγκυκλοπαίδεια Γιοβάνη” | Αθήνα | 1980 |